UMAP

Uniform Manifold Approximation and Projection for Dimension Reduction

Notebook adapted from Anna Poetsch (source) under CC-BY-4.0

Source material:
Tutorial: https://umap-learn.readthedocs.io/en/latest/
Paper: https://arxiv.org/abs/1802.03426

Packages (if not available, pip install):

import numpy as np
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

Load data:

penguins = pd.read_csv("https://github.com/allisonhorst/palmerpenguins/raw/5b5891f01b52ae26ad8cb9755ec93672f49328a8/data/penguins_size.csv")
penguins = penguins.dropna()

Show data:

penguins.head()

	species_short	island	culmen_length_mm	culmen_depth_mm	flipper_length_mm	body_mass_g	sex
0	Adelie	Torgersen	39.1	18.7	181.0	3750.0	MALE
1	Adelie	Torgersen	39.5	17.4	186.0	3800.0	FEMALE
2	Adelie	Torgersen	40.3	18.0	195.0	3250.0	FEMALE
4	Adelie	Torgersen	36.7	19.3	193.0	3450.0	FEMALE
5	Adelie	Torgersen	39.3	20.6	190.0	3650.0	MALE

penguins = penguins.dropna() penguins.species_short.value_counts()

sns.pairplot(penguins, hue='species_short')

<seaborn.axisgrid.PairGrid at 0x7fae38a024f0>

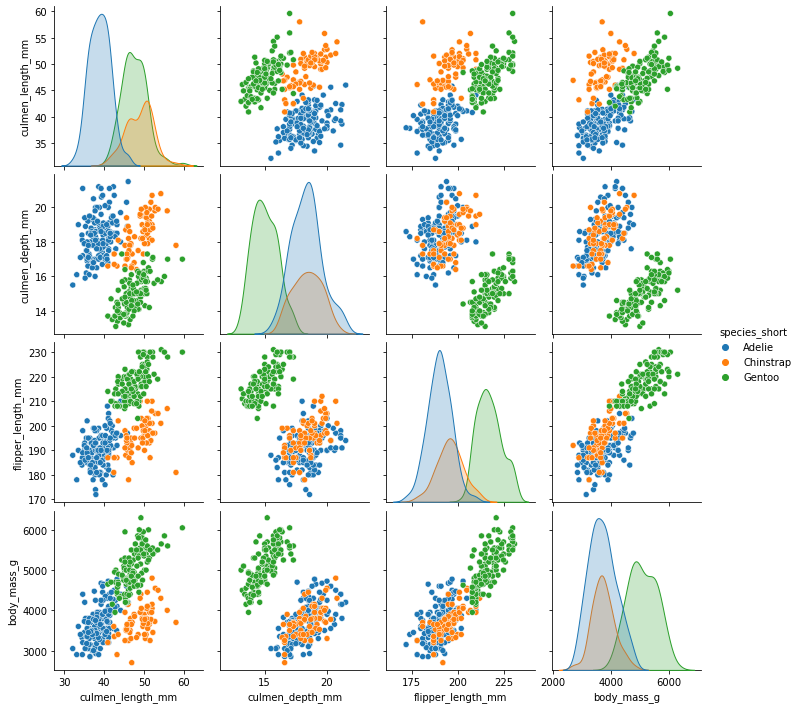
Data scaling

change data format to values:

penguin_data = penguins[
    [
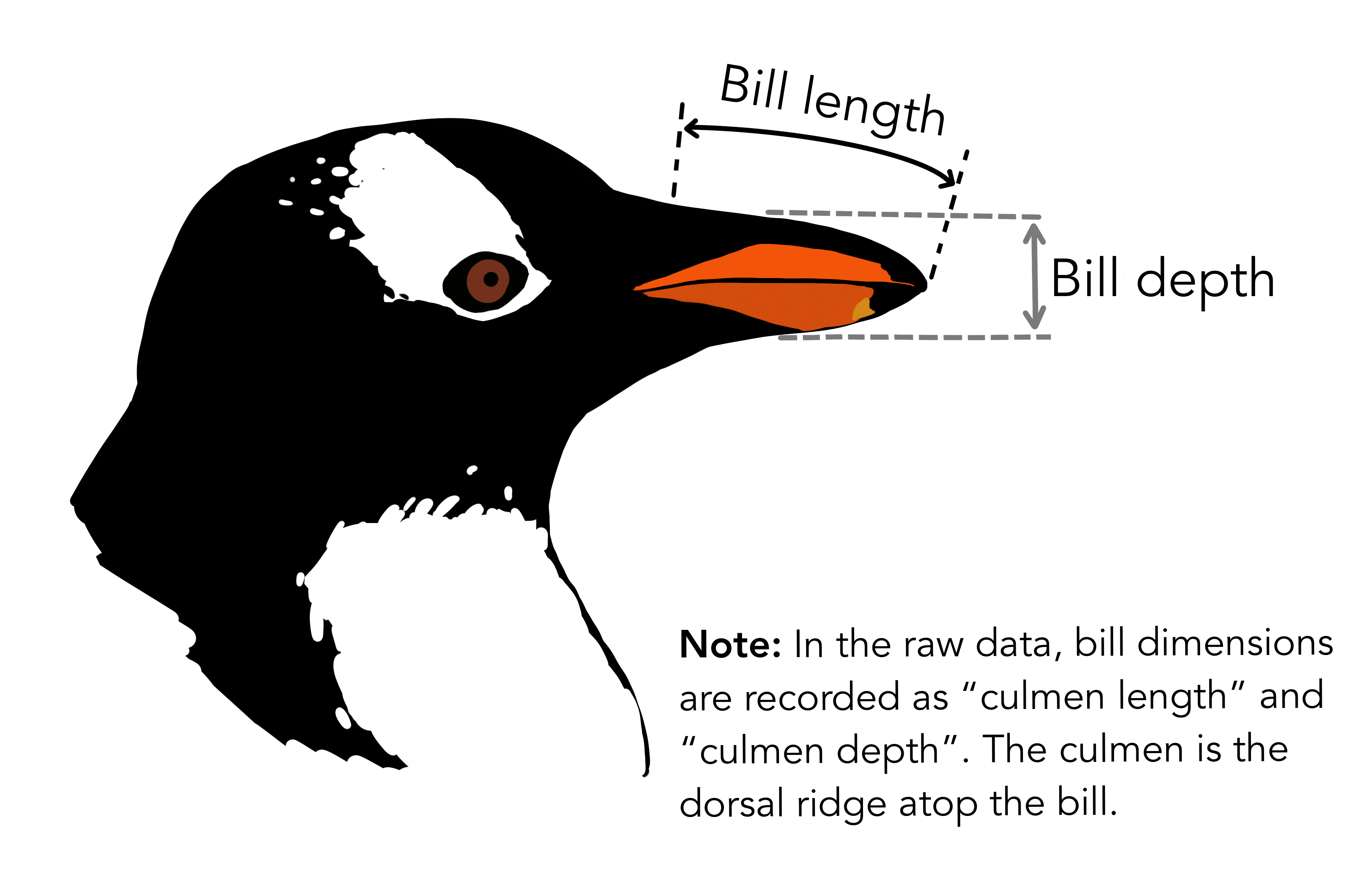
        "culmen_length_mm",
        "culmen_depth_mm",
        "flipper_length_mm",
        "body_mass_g",
    ]
].values

import umap.umap_ as umap #install with 'pip install umap-learn'
np.random.seed(42) #a seed is defined, because there is a random component to UMAP

reducer = umap.UMAP()

scaled_penguin_data = StandardScaler().fit_transform(penguin_data)

scaled_penguin_data

array([[-0.89765322,  0.78348666, -1.42952144, -0.57122888],
       [-0.82429023,  0.12189602, -1.07240838, -0.50901123],
       [-0.67756427,  0.42724555, -0.42960487, -1.19340546],
       ...,
       [ 1.17485108, -0.74326098,  1.49880565,  1.91747742],
       [ 0.22113229, -1.20128527,  0.78457953,  1.23308319],
       [ 1.08314735, -0.53969463,  0.85600214,  1.48195382]])

scaled_df = pd.DataFrame(scaled_penguin_data)

sns.pairplot(scaled_df)

<seaborn.axisgrid.PairGrid at 0x7fae38da70a0>

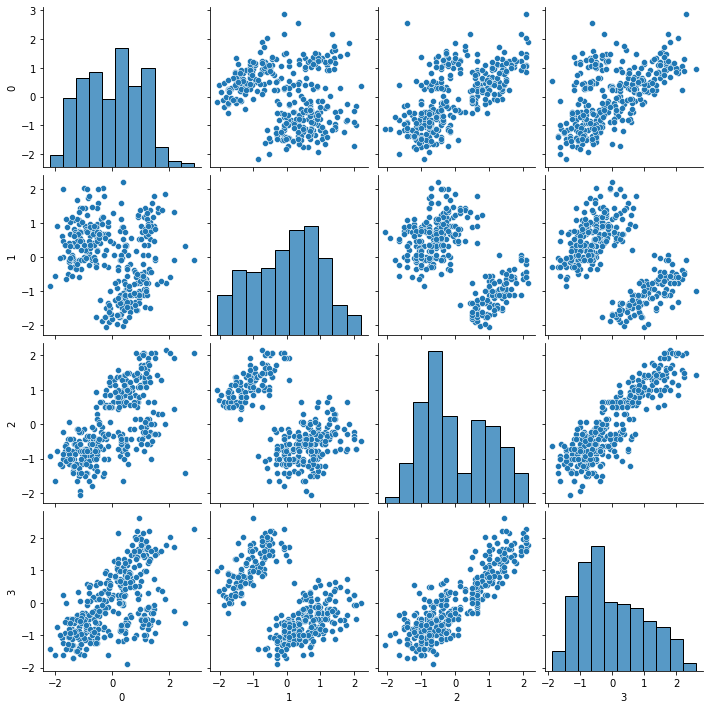
UMAP

embedding = reducer.fit_transform(scaled_penguin_data)
embedding.shape

plt.scatter(
    embedding[:, 0],
    embedding[:, 1],
    c=[sns.color_palette()[x] for x in penguins.species_short.map({"Adelie":0, "Chinstrap":1, "Gentoo":2})])

The separation with UMAP worked generally well, yet there are some Chinstrap penguins that cluster with Gentoo.
Now we can use the two-dimensional embedding to visualise different data:

plt.scatter(
    embedding[:, 0],
    embedding[:, 1],
    c=penguins["culmen_length_mm"])
plt.title("culmen_length_mm")
plt.colorbar()
plt.show()

plt.scatter(
    embedding[:, 0],
    embedding[:, 1],
    c=penguins["culmen_depth_mm"])
plt.title("culmen_depth_mm")
plt.colorbar()
plt.show()

plt.scatter(
    embedding[:, 0],
    embedding[:, 1],
    c=penguins["flipper_length_mm"])
plt.title("flipper_length_mm")
plt.colorbar()
plt.show()

plt.scatter(
    embedding[:, 0],
    embedding[:, 1],
    c=penguins["body_mass_g"])
plt.title("body_mass_g")
plt.colorbar()
plt.show()

n_neighbors

for n in (2, 5, 15, 100, 1000):
    reducer = umap.UMAP(n_neighbors=n)
    embedding = reducer.fit_transform(scaled_penguin_data)
    plt.scatter(
        embedding[:, 0],
        embedding[:, 1],
        c=[sns.color_palette()[x] for x in penguins.species_short.map({"Adelie":0, "Chinstrap":1, "Gentoo":2})]
        )
    plt.title('n_neighbors = {}'.format(n))
    plt.show()

n_neighbors does focus on fine grained structure, when kept small. Then we might miss the bigger picture. When small,it might also generate “sausages”, which can be a reason to want to modify the parameters. The higher one goes, the more cramped the clusters become. One should not define more neighbors than there are data points ;-)

min_dist

for d in (0.0, 0.1, 0.5, 0.9):
    reducer = umap.UMAP(min_dist=d)
    embedding = reducer.fit_transform(scaled_penguin_data)
    plt.scatter(
        embedding[:, 0],
        embedding[:, 1],
        c=[sns.color_palette()[x] for x in penguins.species_short.map({"Adelie":0, "Chinstrap":1, "Gentoo":2})]
        )
    plt.title('min_dist = {}'.format(d))
    plt.show()

min_dist defines how close we allow points to lie on top of each other. The higher the value, the more loose our clusters will be.

metric

for m in ("euclidean","cosine","correlation"):
    reducer = umap.UMAP(metric=m)
    embedding = reducer.fit_transform(scaled_penguin_data)
    plt.scatter(
        embedding[:, 0],
        embedding[:, 1],
        c=[sns.color_palette()[x] for x in penguins.species_short.map({"Adelie":0, "Chinstrap":1, "Gentoo":2})]
        )
    plt.title('metric = {}'.format(m))
    plt.show()

There are many more possibilities to define distances. Eucledian is the default, but one might look for an alternative dependent on the data. For example sparse data, i.e. data with many 0s are frequently addressed with cosine distance. Such data are for example RNA-Seq data.

Randomness

Dont forget, there is a random component as well!
Now we are introducing different seeds, which will change the random component of UMAP

for r in (41,41,42,43):
    np.random.seed(r)
    reducer = umap.UMAP()
    embedding = reducer.fit_transform(scaled_penguin_data)
    plt.scatter(
        embedding[:, 0],
        embedding[:, 1],
        c=[sns.color_palette()[x] for x in penguins.species_short.map({"Adelie":0, "Chinstrap":1, "Gentoo":2})])
    plt.show()

spread

for s in (0.5,1,2):
    reducer = umap.UMAP(spread=s)
    embedding = reducer.fit_transform(scaled_penguin_data)
    plt.scatter(
        embedding[:, 0],
        embedding[:, 1],
        c=[sns.color_palette()[x] for x in penguins.species_short.map({"Adelie":0, "Chinstrap":1, "Gentoo":2})]
        )
    plt.title('spread = {}'.format(s))
    plt.show()

Spread is a parameter that allows increased spread in the two dimensional space. Here it does not make a big difference.