Correlation matrix

In practice (particularly in image analysis) we often calculate a large variety of features that may often be strongly correlated with other features. The introduced correlation coefficients can help us to identify groups of redundant features.

from skimage import data, filters, measure
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

image = data.human_mitosis()

fig, ax = plt.subplots()
ax.imshow(image, cmap='gray')

<matplotlib.image.AxesImage at 0x2481148dbe0>

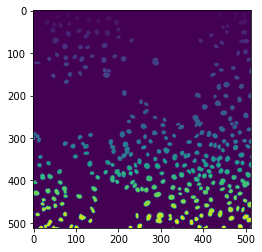
binary = image > filters.threshold_otsu(image)
labels = measure.label(binary)

fig, ax = plt.subplots()
ax.imshow(labels)

<matplotlib.image.AxesImage at 0x2481636d910>

props = measure.regionprops_table(labels, intensity_image=image, properties=['area', 'area_bbox', 'area_convex',
                                                                    'area_filled', 'axis_major_length',
                                                                    'axis_minor_length', 'eccentricity',
                                                                    'equivalent_diameter_area', 'extent',
                                                                    'feret_diameter_max', 'intensity_max',
                                                                    'intensity_mean', 'intensity_min'])
df = pd.DataFrame(props)
df

	area	area_bbox	area_convex	area_filled	axis_major_length	axis_minor_length	eccentricity	equivalent_diameter_area	extent	feret_diameter_max	intensity_max	intensity_mean	intensity_min
0	62	70	63	62	10.571311	7.557049	0.699264	8.884866	0.885714	10.770330	63.0	50.645161	40.0
1	7	7	7	7	8.000000	0.000000	1.000000	2.985411	1.000000	7.000000	68.0	58.285714	39.0
2	121	143	124	121	13.746529	11.516064	0.546064	12.412171	0.846154	14.317821	82.0	61.487603	39.0
3	19	24	20	19	6.674754	3.805741	0.821527	4.918491	0.791667	6.708204	78.0	58.473684	39.0
4	62	80	65	62	11.482908	6.872199	0.801144	8.884866	0.775000	11.661904	86.0	63.387097	42.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...
288	45	60	48	45	11.333091	5.339585	0.882053	7.569398	0.750000	12.041595	102.0	78.533333	42.0
289	49	90	61	49	18.128803	4.509369	0.968570	7.898654	0.544444	18.027756	100.0	73.387755	40.0
290	39	50	42	39	9.496172	5.480726	0.816637	7.046726	0.780000	10.049876	87.0	66.000000	39.0
291	4	4	4	4	4.472136	0.000000	1.000000	2.256758	1.000000	4.000000	59.0	53.750000	45.0
292	4	4	4	4	4.472136	0.000000	1.000000	2.256758	1.000000	4.000000	41.0	40.250000	39.0

293 rows × 13 columns

We can calculate a correlation matrix using a given correlation metric with pandas:

correlation_matrix = df.corr(method='pearson')

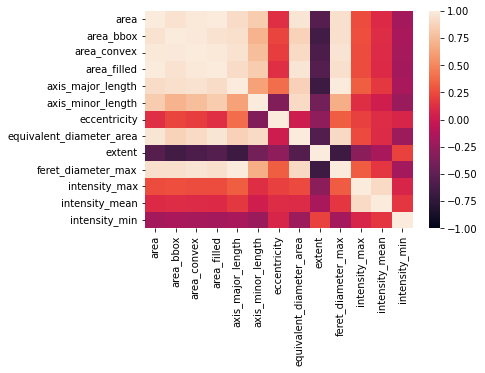
It seems obvious that there is quite a large number of features that are strongly connected to each other - Seaborn offers the heatmap function for this:

ax = sns.heatmap(correlation_matrix, annot=False, vmin=-1, vmax=1)

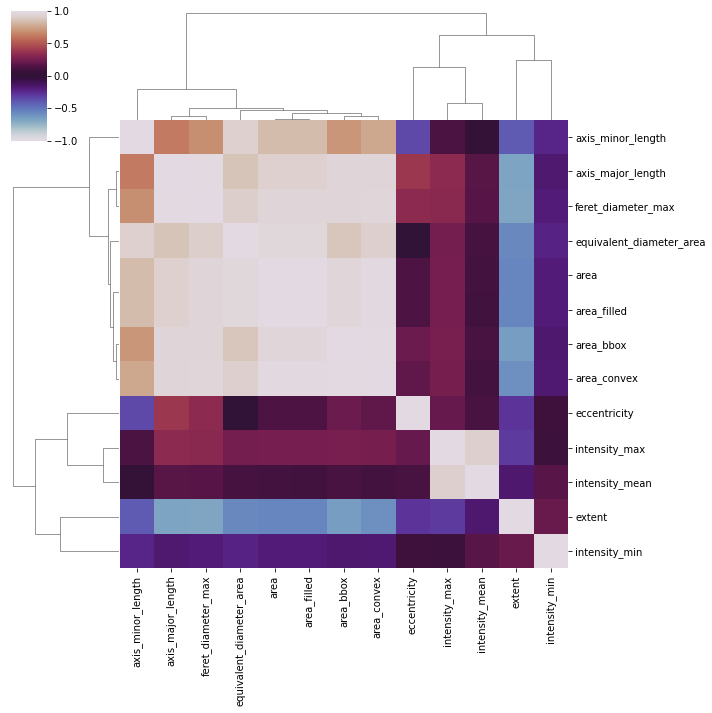
Maybe we can make this even clearer by rearranging some of the columns/rows. We can use the seaborn clustermap feature for this:

fig = sns.clustermap(correlation_matrix, vmin=-1, vmax=1, cmap='twilight')