Nonparametric testing
Contents
Nonparametric testing#
import seaborn as sns
import scipy.stats as st
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.stats.multicomp import pairwise_tukeyhsd
Comparing parametric and non-parametric testing#
To compare parametric and non-parametric testing, lets go back to the example counting white blood cells.
dat = pd.read_csv('../../data/leukocyte_counts.csv')
print(dat)
healthy COVID19 CLL
0 8112.953628 7938.261511 7995.138663
1 8049.767571 8815.331615 7169.552971
2 8092.332735 7830.310038 6780.272875
3 7498.168785 6240.226527 9962.335281
4 7143.005306 7745.239515 7786.586473
.. ... ... ...
95 7034.384604 6599.861270 6572.275825
96 7745.826977 8654.514650 8934.513929
97 8604.575198 8732.430100 7879.404564
98 7131.230127 7676.868854 7464.286189
99 7734.212640 7591.721753 6862.094897
[100 rows x 3 columns]
sns.swarmplot(data=dat)
<AxesSubplot:>
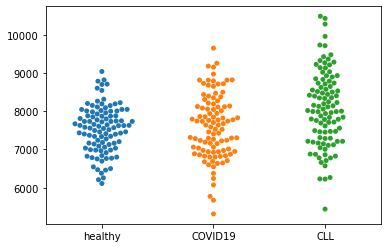
Now to compare healthy with COVID19 we are doing a t-test that compares the mean.
st.ttest_ind(dat['healthy'],dat['COVID19'])
Ttest_indResult(statistic=-0.6672986139650978, pvalue=0.5053583624156102)
The assumption of equal standard deviation was however violated for this test, so maybe we should have taken a non-parametric test?
st.wilcoxon(dat['healthy'],dat['COVID19'])
WilcoxonResult(statistic=2332.0, pvalue=0.506948473287772)
How about the difference healthy-CLL?
st.ttest_ind(dat['healthy'],dat['CLL'])
Ttest_indResult(statistic=-4.695380523297982, pvalue=4.964171715705624e-06)
st.wilcoxon(dat['healthy'],dat['CLL'])
WilcoxonResult(statistic=1283.0, pvalue=1.9512317174970406e-05)
Our p-value is one order of magnitude larger. Why is that?
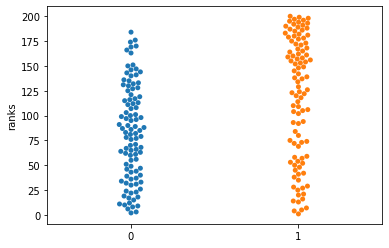
Wilcoxon is comparing the ranks, so some information is lost, which frequently leads to loss of power. What is actually compared? Lets take the ranks.
df4 = st.rankdata(dat[['healthy','CLL']]).reshape(100,2)
sns.swarmplot(data=df4)
plt.ylabel("ranks")
df2 = pd.DataFrame(df4)
print(df2)
0 1
0 136.0 124.0
1 133.0 48.0
2 135.0 20.0
3 76.0 197.0
4 44.0 104.0
.. ... ...
95 36.0 13.0
96 100.0 181.0
97 166.0 114.0
98 43.0 72.0
99 96.0 27.0
[100 rows x 2 columns]
ANOVA#
Now we have three samples, so a t-test is actually not appropriate. If we state the 0-Hypothesis that there is no difference between samples, we should apply a one-way ANOVA.
sns.swarmplot(data=dat)
<AxesSubplot:>
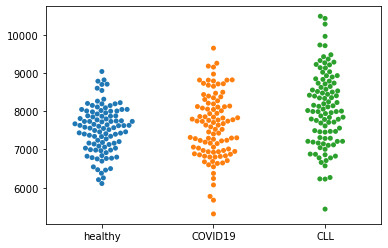
st.f_oneway(dat['healthy'],dat['COVID19'],dat['CLL'])
F_onewayResult(statistic=12.847664465933143, pvalue=4.452663722900786e-06)
Now we know that we can reject H0 that there is no difference between the means in this case
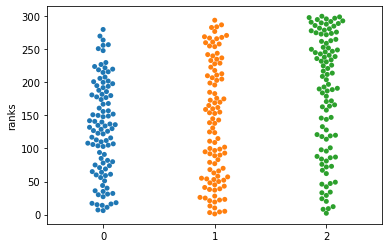
How does this look for a non-parametric situation?
Comparing Kruskal-Wallis with ANOVA#
df4 = st.rankdata(dat).reshape(100,3)
sns.swarmplot(data=df4)
plt.ylabel("ranks")
df2 = pd.DataFrame(df4)
print(df2)
0 1 2
0 208.0 183.0 191.0
1 202.0 267.0 81.0
2 206.0 170.0 33.0
3 122.0 10.0 297.0
4 75.0 155.0 163.0
.. ... ... ...
95 64.0 21.0 20.0
96 156.0 254.0 276.0
97 251.0 261.0 179.0
98 74.0 143.0 118.0
99 149.0 131.0 46.0
[100 rows x 3 columns]
st.kruskal(dat['healthy'],dat['COVID19'],dat['CLL'])
KruskalResult(statistic=20.514054485049883, pvalue=3.5109906089968794e-05)
As before, we are loosing a bit of power. From the ranking plot, it becomes especially clear that we are looking at all comparisons at the same time…. but we really want to know which one makes the difference! But here we need to include Multiple testing correction!
Multiple testing correction#
For ANOVA there is Tukey. For non-parametric tests, there is Dunn’s test.
# For Tukey the dataframe needs to be melted
melted = pd.melt(dat)
print(melted)
# perform multiple pairwise comparison (Tukey HSD)
m_comp = pairwise_tukeyhsd(endog=melted['value'], groups=melted['variable'], alpha=0.05)
print(m_comp)
variable value
0 healthy 8112.953628
1 healthy 8049.767571
2 healthy 8092.332735
3 healthy 7498.168785
4 healthy 7143.005306
.. ... ...
295 CLL 6572.275825
296 CLL 8934.513929
297 CLL 7879.404564
298 CLL 7464.286189
299 CLL 6862.094897
[300 rows x 2 columns]
Multiple Comparison of Means - Tukey HSD, FWER=0.05
===========================================================
group1 group2 meandiff p-adj lower upper reject
-----------------------------------------------------------
CLL COVID19 -475.5107 0.0002 -751.2208 -199.8005 True
CLL healthy -545.0705 0.0 -820.7807 -269.3603 True
COVID19 healthy -69.5598 0.8233 -345.27 206.1504 False
-----------------------------------------------------------
Also in these tests the individual comparisons are not independent, which makes them very suitable for moderately multiple testing correction.
When going “big”, Bonferroni and Benjamini-Hochberg are more custom, which for the former just correct by the total numbers of comparisons and for the latter adjust the false discovery rate (FDR).

