Quantiative neighborhood measurements#

In this notebook we demonstrate how to quantify relationships between neighboring cells. We use the neighbor count to remove objects from a label image that are no cells. Afterwards we will measure and visualize the size of cells and the average size of cells in a given neighborhood.

import pyclesperanto_prototype as cle
import numpy as np
from skimage.io import imread
import pandas as pd

The example image maize_clsm.tif was shared by David Legland and is licensed under CC-BY 4.0 license.

intensity_image = imread('../../data/maize_clsm.tif')
cle.imshow(intensity_image)
../_images/05_quantitative_neighbor_maps_3_0.png

Starting point: Label map#

We use a basic segmentation algorithm to segment the dark objects in the image, hoping these are mostly cells.

binary = cle.binary_not(cle.threshold_otsu(intensity_image))
objects = cle.voronoi_labeling(binary)

cle.imshow(objects, labels=True)
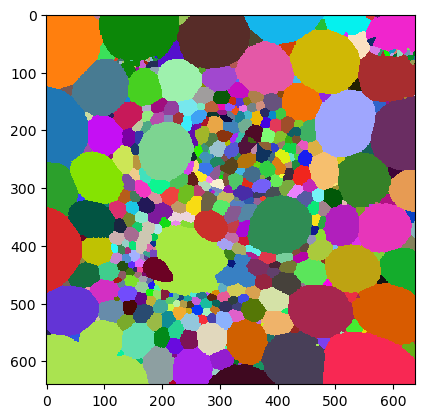
../_images/05_quantitative_neighbor_maps_5_0.png

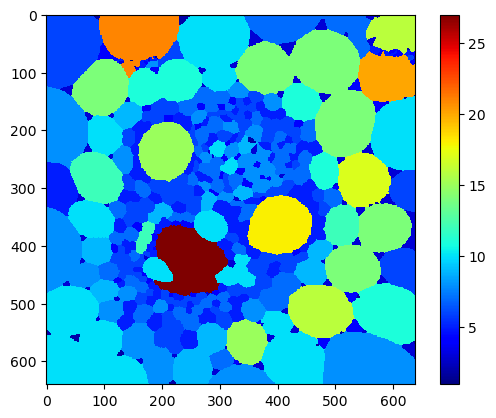
Number of touching neighbor map#

Next, we visualize the number of neighbors in colour.

num_neighbors_map = cle.touching_neighbor_count_map(objects)

cle.imshow(num_neighbors_map, 
           colormap='jet', 
           colorbar=True)
../_images/05_quantitative_neighbor_maps_7_0.png

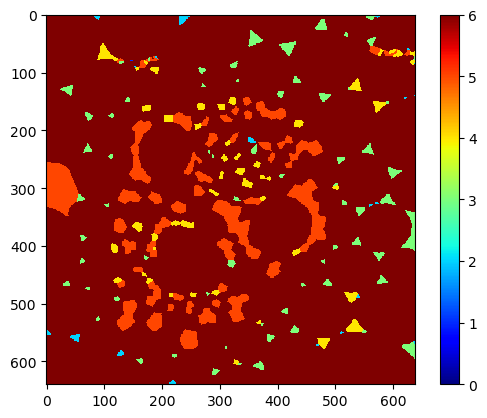
By specifying minimum and maximum display intensity, we can see that most triangular objects, that are presumably no cells, have about 3 neighbors only.

cle.imshow(num_neighbors_map, 
           min_display_intensity=0, 
           max_display_intensity=6, 
           colormap='jet', 
           colorbar=True)
../_images/05_quantitative_neighbor_maps_9_0.png

Filtering labels according to measurements#

We can now exclude objects that have < 4 neighbors.

cells = cle.exclude_labels_with_map_values_out_of_range(num_neighbors_map, objects, minimum_value_range=4)

cle.imshow(cells, labels=True)
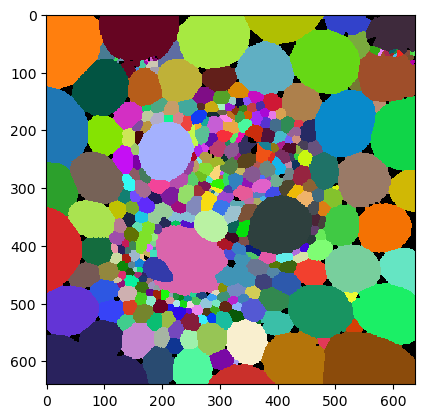
../_images/05_quantitative_neighbor_maps_11_0.png

Averaging values over a defined neighborhood#

Now, with a cleaned result, we can measure properties of cells. Note: It would be scientifically questionable to count the number of neighbors now as we used this measurement for filtering the objects.

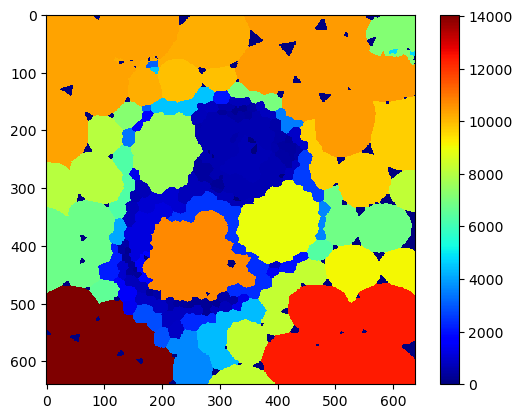
area_map = cle.pixel_count_map(cells)
cle.imshow(area_map, 
           colormap='jet', 
           colorbar=True)
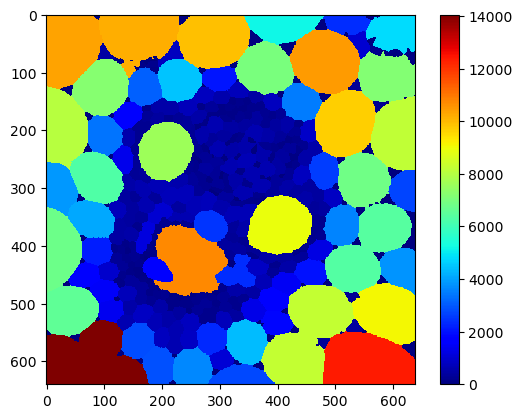
../_images/05_quantitative_neighbor_maps_13_0.png

For visualization purposes, we now produce a map that shows the average size and the maximum among neighbors for each cell.

local_mean_area_map = cle.mean_of_touching_neighbors_map(area_map, cells)
cle.imshow(local_mean_area_map, 
           colormap='jet', 
           colorbar=True)
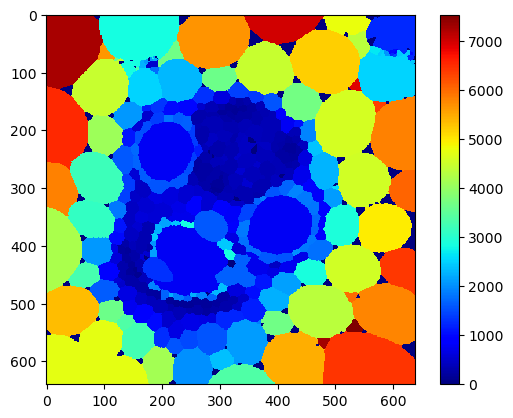
../_images/05_quantitative_neighbor_maps_15_0.png 
local_max_area_map = cle.maximum_of_touching_neighbors_map(area_map, cells)
cle.imshow(local_max_area_map, 
           colormap='jet', 
           colorbar=True)
../_images/05_quantitative_neighbor_maps_16_0.png

Tabular neighborhood analysis#

These and similar measurments can also be derived in tabular form.

statistics = cle.statistics_of_labelled_neighbors(cells)

pd.DataFrame(statistics)
label touching_neighbor_count minimum_distance_of_touching_neighbors average_distance_of_touching_neighbors maximum_distance_of_touching_neighbors max_min_distance_ratio_of_touching_neighbors proximal_neighbor_count_d10 proximal_neighbor_count_d20 proximal_neighbor_count_d40 proximal_neighbor_count_d80 ... touching_neighbor_count_dilated_r_10 minimum_distance_of_touching_neighbors_dilated_r_10 average_distance_of_touching_neighbors_dilated_r_10 maximum_distance_of_touching_neighbors_dilated_r_10 max_min_distance_ratio_of_touching_neighbors_dilated_r_10 touch_count_sum_dilated_r_10 minimum_touch_count_dilated_r_10 maximum_touch_count_dilated_r_10 minimum_touch_portion_dilated_r_10 maximum_touch_portion_dilated_r_10
0 1 4.0 60.320210 101.840363 139.683594 2.315701 0.0 0.0 0.0 1.0 ... 4.0 60.131992 101.611427 138.916809 2.310198 251.0 40.0 99.0 0.159363 0.394422
1 2 5.0 70.345596 102.279503 139.683594 1.985676 0.0 0.0 0.0 1.0 ... 5.0 69.458466 101.834366 138.916809 1.999998 313.0 47.0 81.0 0.150160 0.258786
2 3 4.0 66.247681 88.231575 105.587234 1.593825 0.0 0.0 0.0 2.0 ... 4.0 65.842422 88.179047 105.653221 1.604638 231.0 54.0 67.0 0.233766 0.290043
3 4 5.0 62.034245 82.326614 107.360519 1.730665 0.0 0.0 0.0 3.0 ... 5.0 61.471870 82.060867 107.331879 1.746032 283.0 46.0 66.0 0.162544 0.233216
4 5 5.0 65.249962 80.454788 107.360519 1.645373 0.0 0.0 0.0 3.0 ... 5.0 65.238731 80.336967 107.331879 1.645217 309.0 32.0 132.0 0.103560 0.427184
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
369 370 4.0 6.401806 28.644737 55.443081 8.660537 2.0 5.0 10.0 14.0 ... 4.0 6.355856 29.127771 55.813652 8.781452 46.0 6.0 25.0 0.130435 0.543478
370 371 5.0 7.438875 17.765903 53.682270 7.216450 4.0 4.0 9.0 14.0 ... 5.0 7.462044 17.792099 54.364231 7.285434 50.0 5.0 16.0 0.100000 0.320000
371 372 4.0 5.430400 16.685814 47.472179 8.741931 3.0 4.0 9.0 14.0 ... 4.0 5.702640 17.013132 48.531986 8.510442 26.0 5.0 8.0 0.192308 0.307692
372 373 2.0 8.850188 30.322327 51.794464 5.852357 1.0 4.0 9.0 14.0 ... 2.0 8.285303 30.604389 52.923477 6.387633 36.0 16.0 20.0 0.444444 0.555556
373 374 3.0 5.430400 22.109964 51.449951 9.474431 2.0 4.0 9.0 14.0 ... 3.0 5.702640 22.457144 53.156166 9.321326 23.0 6.0 10.0 0.260870 0.434783

374 rows × 64 columns