Scientific plotting with seaborn

In this tutorial, we will use some of the measurements taken in the course and visualize them nicely using the seaborn Python library. Seaborn comes with the advantage that it interacts very nicely with the DataFrame format from the Python pandas library - a convenient way of handling tabular data in Python.

For more detailed information: You may have been used to using Matplotlib for plotting in Python. In a way, seaborn is just matplotlib - but it expands the functionality of matplotlib to be easier to use for more complex visualizations.

Let’s load all the packages we need here:

import seaborn as sns
import os
import pandas as pd

Loading the data

As a first step, we need to load the measurements from napari. Alternatively, you can download some from the course repository (TODO: Add link). For this, we need to compile a list of all .csv files we takr into account.

root = r'./measurements'

files = os.listdir(root)
files

['17P1_POS0006_D_1UL_labels.csv',
 '17P1_POS0007_D_1UL_labels.csv',
 '17P1_POS0011_D_1UL_labels.csv',
 '20P1_POS0005_D_1UL_labels.csv',
 '20P1_POS0007_D_1UL_labels.csv',
 '20P1_POS0008_D_1UL_labels.csv',
 '20P1_POS0010_D_1UL_labels.csv',
 'A9_p5d_labels.csv',
 'A9_p7d_labels.csv',
 'A9_p9d_labels.csv']

Next, we load them all into pandas dataframes. For this, we go through the data in a for-loop, load each file and then concatenate all the tabular data into a single table. Let’s look into a single dataframe first to see what we are dealing with. The df.head(5) command shows us the first 5 rows of the table so that we don’t clutter our output with tons of tabular data:

first_file = os.path.join(root, files[0])
df = pd.read_csv(first_file)
df.head(5)

	Unnamed: 0	label	area_filled	perimeter	axis_major_length	axis_minor_length	eccentricity	area	intensity_mean	intensity_max	intensity_min	index
0	0	1	29.0	18.863961	7.853437	4.935022	0.777898	29.0	58.724138	67.0	49.0	1
1	1	2	32.0	24.242641	12.953143	3.174186	0.969510	32.0	73.343750	118.0	40.0	2
2	2	3	316.0	65.112698	22.947857	17.642785	0.639465	316.0	95.332278	248.0	22.0	3
3	3	4	258.0	60.284271	22.477335	14.716400	0.755870	258.0	113.585271	204.0	19.0	4
4	4	5	59.0	32.278175	15.198125	5.328297	0.936529	59.0	80.881356	162.0	35.0	5

We notice that there’s a bunch of irrelevant stuff. The index column is a remnant of the analysis in napari - so let’s drop it:

df.drop(columns=['index']).head(5)

	Unnamed: 0	label	area_filled	perimeter	axis_major_length	axis_minor_length	eccentricity	area	intensity_mean	intensity_max	intensity_min
0	0	1	29.0	18.863961	7.853437	4.935022	0.777898	29.0	58.724138	67.0	49.0
1	1	2	32.0	24.242641	12.953143	3.174186	0.969510	32.0	73.343750	118.0	40.0
2	2	3	316.0	65.112698	22.947857	17.642785	0.639465	316.0	95.332278	248.0	22.0
3	3	4	258.0	60.284271	22.477335	14.716400	0.755870	258.0	113.585271	204.0	19.0
4	4	5	59.0	32.278175	15.198125	5.328297	0.936529	59.0	80.881356	162.0	35.0

The Unnamed: 0 column is essentially just the row index of the csv file, which pandas loads by default, but doesn’t know where to put it. We can tell pandas to use this column as the index of the row upon import. Let’s load everything now!

Hint We may want to distinguish from which dataset which measurement came. To do so, we simply add another column to each dataframe, that indicates from whhich image the respective measurement comes

big_df = pd.DataFrame()

for file in files:
    full_filename = os.path.join(root, file)
    df = pd.read_csv(full_filename, index_col='Unnamed: 0')  #load dataframe
    df = df.drop(columns=['index'])  # drop irrelevant index column
    df['sample'] = file  # add column with sample name

    big_df = pd.concat([big_df, df], axis=0)  # append table to big_df

big_df

	label	area_filled	perimeter	axis_major_length	axis_minor_length	eccentricity	area	intensity_mean	intensity_max	intensity_min	sample
0	1	29.0	18.863961	7.853437	4.935022	0.777898	29.0	58.724138	67.0	49.0	17P1_POS0006_D_1UL_labels.csv
1	2	32.0	24.242641	12.953143	3.174186	0.969510	32.0	73.343750	118.0	40.0	17P1_POS0006_D_1UL_labels.csv
2	3	316.0	65.112698	22.947857	17.642785	0.639465	316.0	95.332278	248.0	22.0	17P1_POS0006_D_1UL_labels.csv
3	4	258.0	60.284271	22.477335	14.716400	0.755870	258.0	113.585271	204.0	19.0	17P1_POS0006_D_1UL_labels.csv
4	5	59.0	32.278175	15.198125	5.328297	0.936529	59.0	80.881356	162.0	35.0	17P1_POS0006_D_1UL_labels.csv
...	...	...	...	...	...	...	...	...	...	...	...
102	103	509.0	91.597980	34.431846	19.886244	0.816353	509.0	59.245580	118.0	31.0	A9_p9d_labels.csv
103	104	87.0	41.106602	18.743849	6.228837	0.943169	87.0	72.103448	138.0	25.0	A9_p9d_labels.csv
104	105	129.0	46.727922	20.222045	8.532153	0.906632	129.0	80.813953	126.0	26.0	A9_p9d_labels.csv
105	106	196.0	54.142136	20.214850	12.912128	0.769419	196.0	80.387755	171.0	21.0	A9_p9d_labels.csv
106	107	30.0	21.071068	9.779252	4.102249	0.907762	30.0	62.700000	83.0	37.0	A9_p9d_labels.csv

883 rows × 11 columns

From the data here we can see that there are three different sample types - A9, 17P1 and 20P1. Let’s add a column to the dataframe tahat indicates from which type the respective image was taken:

big_df['experiment'] = big_df['sample'].apply(lambda x: x.split('_')[0])
big_df.head()

	label	area_filled	perimeter	axis_major_length	axis_minor_length	eccentricity	area	intensity_mean	intensity_max	intensity_min	sample	experiment
0	1	29.0	18.863961	7.853437	4.935022	0.777898	29.0	58.724138	67.0	49.0	17P1_POS0006_D_1UL_labels.csv	17P1
1	2	32.0	24.242641	12.953143	3.174186	0.969510	32.0	73.343750	118.0	40.0	17P1_POS0006_D_1UL_labels.csv	17P1
2	3	316.0	65.112698	22.947857	17.642785	0.639465	316.0	95.332278	248.0	22.0	17P1_POS0006_D_1UL_labels.csv	17P1
3	4	258.0	60.284271	22.477335	14.716400	0.755870	258.0	113.585271	204.0	19.0	17P1_POS0006_D_1UL_labels.csv	17P1
4	5	59.0	32.278175	15.198125	5.328297	0.936529	59.0	80.881356	162.0	35.0	17P1_POS0006_D_1UL_labels.csv	17P1

Plotting: Distributions

Now for the actual plotting: Let’s try it with a histogram of the nuclei sizes first. The seaborn syntax is very simple: We pass the measurements table big_df directly to the plotting function (sns.histplot) and tell seaborn which variable to take into account for the histogram.

sns.histplot(data=big_df, x='area_filled', bins=100)

<Axes: xlabel='area_filled', ylabel='Count'>

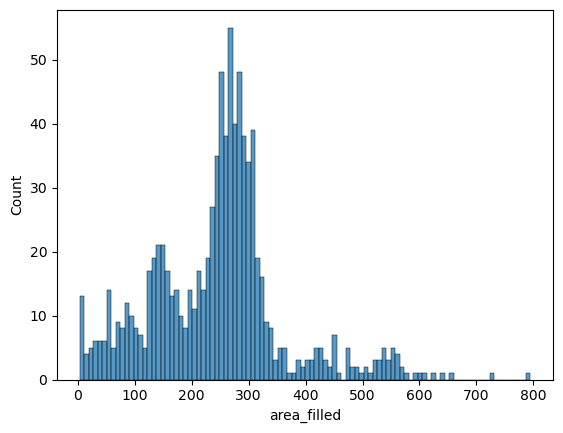
Seaborn also offers to turn this into a smoothed distribution estimate (a kernel-density estimation):

sns.histplot(data=big_df, x='area_filled', bins=100, kde=True)

<Axes: xlabel='area_filled', ylabel='Count'>

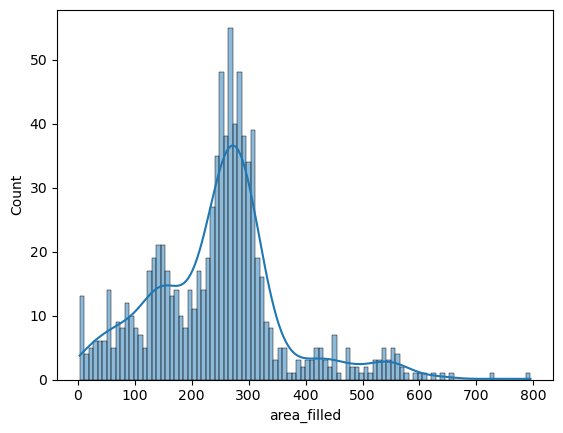
But where seaborn really shines, is when it comes to comparing different groups in datasets (i.e., categorical variables). If we wanted to compare directly how the nuclei sizes differ between the different conditions (i.e., images), we can simply pass this on to seaborn as the hue parameter:

sns.histplot(data=big_df, x='area_filled', hue='sample', kde=True)

<Axes: xlabel='area_filled', ylabel='Count'>

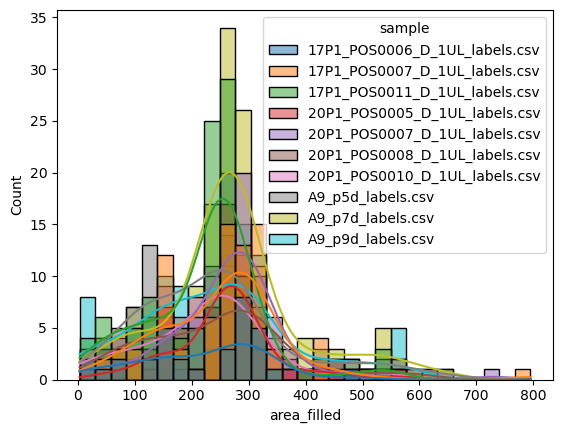
Let’s replace the sample as the category by the experiment column:

sns.histplot(data=big_df, x='area_filled', hue='experiment', kde=True)

<Axes: xlabel='area_filled', ylabel='Count'>

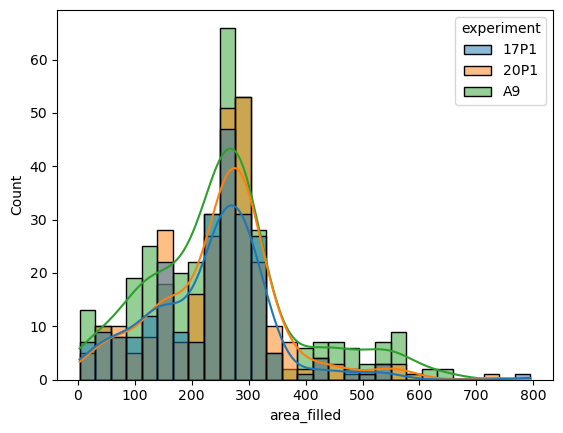
If you only ewant the smoothed histogram estimations rather than the bars, consider using the kdeplot function rather than the histogram:

sns.kdeplot(data=big_df, x='area_filled', hue='sample')

<Axes: xlabel='area_filled', ylabel='Density'>

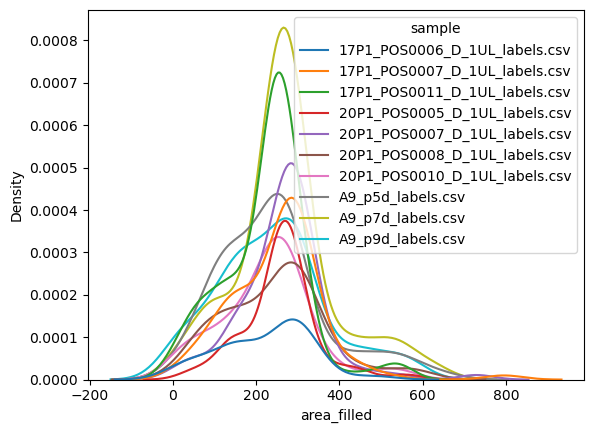
Plotting: Scatters

For a more granular insight into the individual data points, let’s take one step back and draw a good old scatterplot and draw two of the above variables against ech other:

sns.scatterplot(data=big_df, x='area_filled', y='eccentricity')

<Axes: xlabel='area_filled', ylabel='eccentricity'>

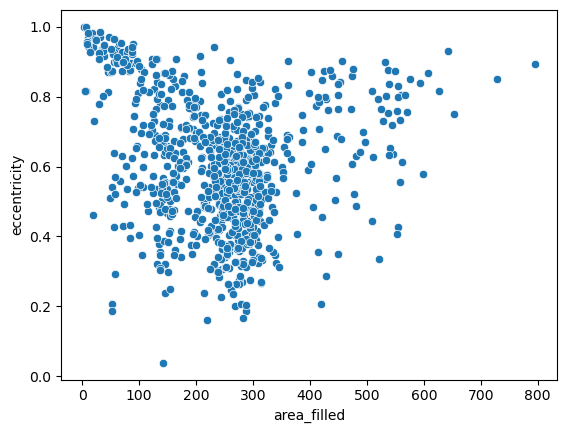
Again, we can simply pass a categorical variable as hue parameter and highlight the different samples. Let’s look at a different property:

sns.scatterplot(data=big_df, x='intensity_mean', y='eccentricity', hue='experiment')

<Axes: xlabel='intensity_mean', ylabel='eccentricity'>

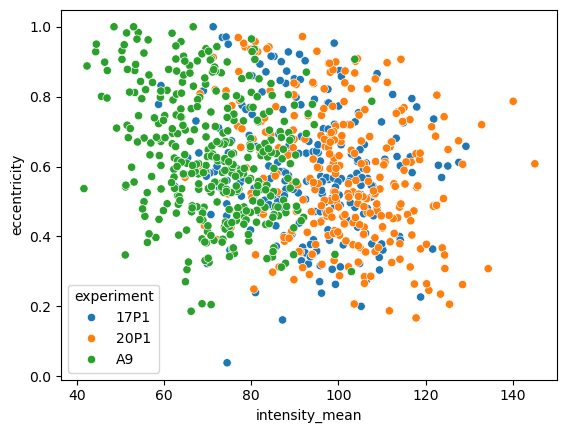
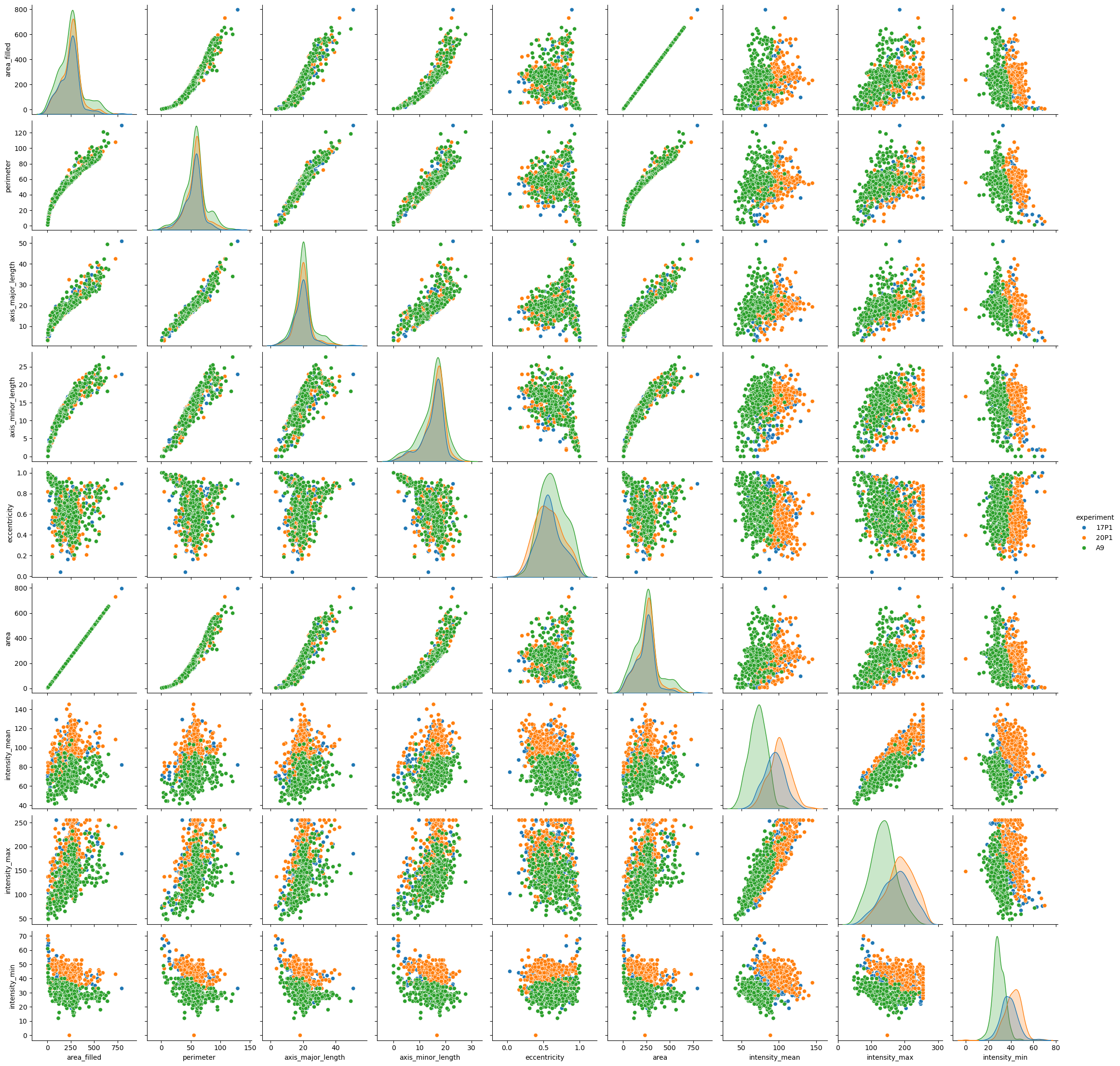
For a smaller number of features, you may want to plot everything against everything - something that may be terribly hard to do in matplotlib. We drop the label column, though - it holds no information about any relevant biology:

sns.pairplot(data=big_df.drop(columns=['label']), hue='experiment')

<seaborn.axisgrid.PairGrid at 0x1fecb2a4c10>